이번에는
"탄성계수와 전단탄성계수의 관계"에 대해서
설명하겠습니다.
전공시험자나 아니면,
일반기계기사 시험을 준비하시는 입장에서는
탄성계수와 전단탄성계수의 관계식은
암기하시는 것이 낫다고 생각합니다.
왜냐하면 증명할 때 가정은
전단상태인데,
이 상태에서 식을 2개 가져오는 것을 기억하는 것이
쉽지는 않기 때문입니다.
게다가 고등학교 때 배운 코사인 법칙도 사용되니
더더욱 기억하는 것은 쉽지 않습니다.
이것을 수치적으로 계산하고 증명하는 것도 마찬가지입니다.
그래서 저는
이 "탄성계수와 전단탄성 계수의 관계"에 대해서는
관계식이
어떠한 상황에서 유도되고,
그 상황에서 쓸 수 있는 식이 무엇이 나오는지
그리고, 어떻게 계산되는지만
눈으로 이해하시면 됩니다.
여기까지는 설계나 개발, 해석자분들께 추천드리는 것이고,
대학원 이상이나 더 깊은 연구에
몰두하시는 분이시라면,
저는 이 식이 유도되는 것이
어렵지 않으니
연습하시는 것을 추천드립니다.
※ 이번 포스팅의 소제목 내부링크
2. 비틀림 기본개념 (8) - 불균일 비틀림 (링크)
1. 탄성계수와 전단탄성계수의 관계
먼저 한 구조물이 순수전단 또는 비틀림 상태에 있다고 가정하겠습니다.

여기서 2가지 식을 가져오겠습니다.
대각선BD의 길이
그리고, 대각선 BD입장에서 길이방향으로 변형이 생겨서
발생한 수직변형률에 대한 식입니다.

전단변형된 사각형을 대각선 BD로 나눠 삼각형으로 보고,
변BD에 대해 제2코사인 법칙을 세우면 아래와 같습니다.(식③)

거기에 ① 식을 식 ③에 대입합니다.
정리하면 아래와 같습니다.

(참고 1)
(전단변형률은 각도가 작기 때문에 각도 크기값이 sin, tan값과
수치적으로 크게 다를바 없습니다.)
(참고 2)
(변형률 자체 값이 작은데, 거기에 제곱을 한다면, 수치적으로 매우 작기 때문에 0으로 취급합니다.)
최대수직변형률이 전단변형률의 절반이라는 식에서
전단변형률에 전단응력을 넣고, 식②를 대입해서
전단탄성계수에 대해 정리하면 아래와 같습니다.
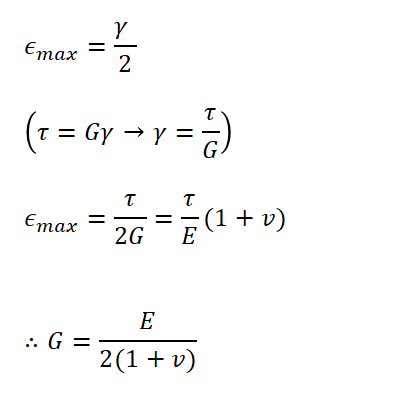
전단탄성계수와 탄성계수의 식의 관계는
순수전단상태에서 전단변형된 요소의 삼각형으로 증명한 것입니다.
만약, 일반기계기사의 시험을 위해서라면,
그냥 전단탄성계수와 탄성계수 증명에서 마지막에 나온 공식을 외우는 것이 낫습니다.
다음에는 불균일 비틀림에 대해서 설명하겠습니다.
2. 비틀림 기본개념 (8) - 불균일 비틀림 (링크)
불균일 단면 또는 단면따라 토크가 변하는 상태에서의
비틀림을 구하는 내용입니다.
자세한 것은 링크를 참고하기 바랍니다.
앞으로도 엔지니어에게 좋은 지식과 정보를 이해하기 쉽게 글을 포스팅하겠습니다. (By. 요르문간드)
'설계지식-재료&구조 > 재료역학(기본)' 카테고리의 다른 글
| 비틀림 기본개념 (4) - 불균일 비틀림 (0) | 2024.03.29 |
|---|---|
| 비틀림 기본개념 (3) - 순수전단(Pure Shear)에 대한 개념 (0) | 2024.03.28 |
| 비틀림 기본개념 (2) - 비틀림각 공식과 강성도, 원형관 공식 (0) | 2024.03.27 |
| 비틀림 기본개념 (1) - 비틀림 개념과 전단변형률, 전단응력 (1) | 2024.03.25 |
| 평면응력 공식 쉽게 이해하기 (0) | 2024.03.21 |





댓글