이번에는
저번에 이어서 극좌표의 단위벡터 미분 중
나머지 하나 각도단위벡터(e_θ)의 미분에 대해 포스팅 하겠습니다.
※ 이번 포스팅의 소제목 내부링크
1. 각도 단위벡터(e_θ)의 미분

각도 단위 벡터를 시간에 대해 미분할 시,
분자,분모에 (dθ)를 곱해서 표현하면 위의 그림같이 됩니다.
각도가 시간에 변하는 dθ/dt는 존재하기 때문에
우리는 "d(e_θ)/dθ"의 값만 구하면 됩니다.
2. "d(e_θ)/dθ"의 정의
"d(e_θ)/dθ"를 즉, 각도단위벡터를 각도로 미분한 것을
극한으로 표현하면 아래와 같습니다.

이를 극좌표계로 표현하면, 분자 값이 부채꼴 궤적(∆s)이 되는데(∆θ는 약분),
이를 최소화(미분)하면, 반시계방향의 미소벡터가 생깁니다.
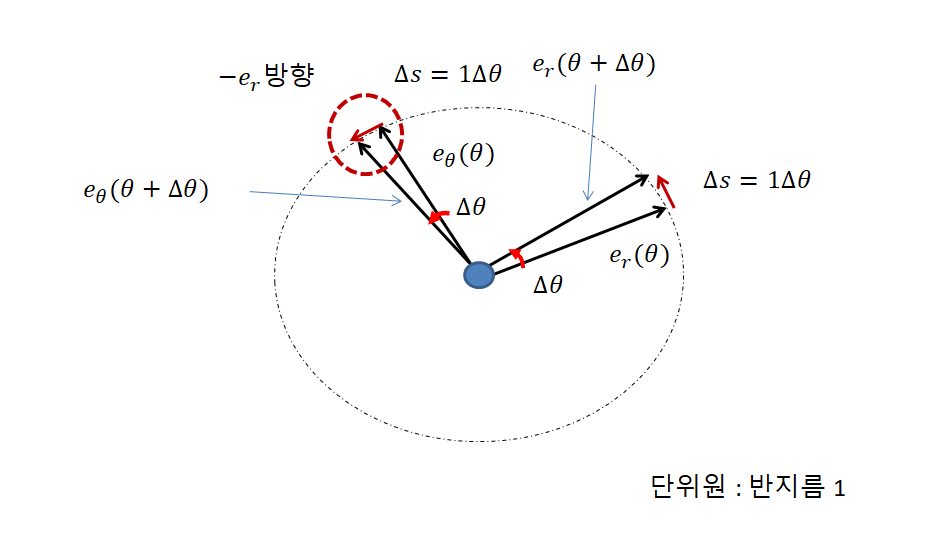
즉, 이 방향은 앞서 포스팅한 "e_r"의 반대방향 : "-(e_r)"과도 같습니다.
극좌표 단위벡터에 모르시거나 기억이 나지 않으시다면,
아래의 이전 포스팅 링크를 참고하기 바랍니다.
3. 동역학 단위벡터 의미 (링크)
[동역학 기본개념] 극좌표의 단위벡터 의미
이번에는 동역학에서의 "극좌표의 단위벡터에 대한 의미"를 주제로 포스팅 하겠습니다. ※ 이번 포스팅의 소제목 내부링크 1. 동역학 에서의 극좌표 벡터 2. 극좌표 벡터 : 거리벡터 (e_r)의 의미 3
archive-engineer-latias21.tistory.com
단위 벡터의 개념을 보고 이 포스팅을 읽는 것을 참고하기 바랍니다.
4. 극좌표 거리 단위벡터(e_θ)의 미분 결론
따라서, 결론은 아래와 같습니다.
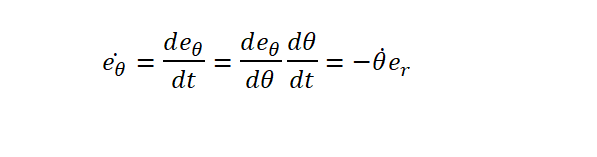
"-"의 부호는 극좌표 반대방향으로 생긴 것이라고 위에 언급하였습니다.
극좌표의 개념과 각 단위벡터의 미분(e_r), (e_θ)의 대해 포스팅 하였습니다.
이렇게 배운 것을 기반으로 각 속도와 가속도에 대한 미분이 나오는 것을 이해 할 수 있습니다.
다음에는" 극좌표계에서의 속도와 가속도에 대한 미분 공식"에 대해 포스팅 하겠습니다.
5. 극좌표계에서 속도, 가속도 미분 공식 (링크)
극좌표 단위벡터가 왜 이렇게 나오는지 알았으니,
다음 포스팅의 공식을 쉽게 이해 또는 암기 할 수 있습니다.
공식에 대해 알고싶다면 링크를 참고하기 바랍니다.
앞으로도 엔지니어에게 좋은 지식과 정보를 이해하기 쉽게 포스팅하겠습니다. (By. 요르문간드)
'설계지식-동역학&진동&제어 > 동역학' 카테고리의 다른 글
| [동역학 기본개념] 접선, 법선 좌표계의 개념 (0) | 2023.06.30 |
|---|---|
| 극좌표계 질점의 속도, 가속도의 공식 (1) | 2023.06.29 |
| [동역학 기본개념] 극좌표 거리 단위벡터(e_r)의 미분의 개념 (0) | 2023.06.27 |
| [동역학 기본개념] 극좌표의 단위벡터 의미 (0) | 2023.06.26 |
| (동역학 기본) 속도, 가속도의 미분활용 (0) | 2023.06.22 |





댓글